Smart Lab Life

シェア

Tweet

第2回 データの位置とばらつきを可視化しよう

バケツとサーチライト：データを読むための姿勢

私たち人間（ヒト）は何も書かれていない “白紙” としてこの世に生を受けてきたわけではありません．生物としてのヒトがその進化の過程で獲得してきたさまざまな“認知的性向”はかつては生存上きっと必要な特性だったでしょう．現代人にもまちがいなく受け継がれているこの進化的遺産を否定するのではなく，逆にうまく使うことが統計学的なデータ解析の前提です．

もちろん，ヒトのもつ認知能力は完全ではありません．バイアスがかかることもあれば，誤りを犯すこともまれではありません．ヒトがもつこれらの“生得的認知”のありようを否定的に見るとしたら，観察者である私たちは客観的に現象やデータを見ることはもはや不可能です．しかし，実は完璧な客観性は統計学がめざす究極の目標ではありません．むしろ，限られたデータからいかにして妥当な結論を導き出すかが統計的推論のゴールです．そのためには，データをいかにうまく読みとって情報を検出できるかという点に関心が向けられるべきでしょう．

得られたデータをしっかり「読む」ことはデータ解析の出発点です．統計分析といえば，つい数式を用いて複雑な「計算」をすることばかりに目が向きがちですが，それは根本的にまちがっています．あらゆる「計算」をする前に，私たちはデータを「読む」必要があります．データを「読む」という観点からいえば，わたしたちがもっている“生得的認知”の能力は積極的に役に立つ武器になりえます．以下では，データを 「読む」 ための直感的方法の重要性についてお話ししましょう．

前回のポイントは，一言でいえば，観察データをしっかり「見る」ことがデータ解析の出発点であるということでした．散布図・幹葉表示・箱ひげ図などさまざまな統計グラフィクスをうまく利用するならば，私たちが生まれつきもっている直感的な認知能力を頼りにして，数値だけでは把握しきれないデータのふるまいを視覚的に理解できるでしょう．難解な数学を理解しなければ一歩も先に進めないとあきらめるのは早計です．

しかし，ここで一つ問題になるのは，「データをよく見ろ」 と言われたとき，私たちは「何」を見ているのかをけっして自覚しているわけではないという点です．データセットのもつどのような特徴を私たちは読みとっているのでしょうか．

たとえば，次のような質問を受けたことがあります：

いずれの質問からも，生のデータを目の前にした観察者が「何」を観察すればいいのかわからずに迷っているようすがうかがえます．確かに，実験なり観察をすればデータは得られます．しかし，データセットさえあれば自動的（受動的）にしかるべき情報が私たちに流れ込んでくるわけではありません．むしろ，観察者たる私たちは自発的（積極的）にデータから情報を読みとろうとする姿勢が必要です．

かつて，科学哲学者カール・R・ポパーはその著書『客観的知識：進化論的アプローチ』（文献2）の中で，科学的知識の獲得に関する「バケツ理論」と「サーチライト理論」とを対置させました．前者の「バケツ理論」とは，人間の五感によって知覚された観察を“バケツ”に貯めこんでいくことが知識を構成するという素朴な考え方です．ポパーは，蓄積された観察さえあればほかは何もいらないという「バケツ理論」に反対し，観察する前に私たちは検証すべき仮説を立てるべきであるとする「サーチライト理論」を提唱しました．ポパーの「サーチライト理論」によれば，

いかなる種類の観察をなすべきか ―われわれの注意をどこに向けるべきか，どの点に関心をもつべきか ―をわれわれが学びとるのは，もっぱら仮説からだけである（文献2，p.2より引用）．

となります．データ解析に当てはめるならば，私たちは単にデータを“バケツ”に受動的に溜め込むのではなく，データセットを能動的に「読む」ための“サーチライト”を用意しなければなりません．いったいデータの「何」に光を当てればいいのでしょうか？

分布の位置とばらつきを可視化する

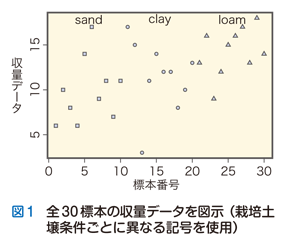
ここで，データは「変動する（ばらつく）」という真理に注目しましょう．たとえば生物を対象とする実験ならば，コントロールされた実験要因はもちろん，遺伝的変動あるいは環境的変動により，観察データにはばらつきが生じます．たとえば，前回用いた事例である栽培土壌条件を変えたときのある作物収量データを再びとり上げましょう．3通りの栽培土壌条件（「clay」 ＝粘土 ／ 「loam」 ＝ ローム ／ 「sand」 ＝ 砂）によってある作物の収量を10標本ずつ調査したデータをインデックス・プロットとして図示すると図1のようになります．

全データを何の手も加えずに可視化した図1をじっと観察するうちに，私たちはこのデータセットがもつ特徴に光を当てる “サーチライト” がいくつかあることに気づきます．まずはじめに，複数のデータの“真ん中”を計算することによりデータセットのおおまかな「位置付け」ができます．前回とり上げた箱ひげ図ではこの“真ん中”を中央値（メディアン）によって示しました．以下では，中央値の代わりに，データセットの平均値（mean）すなわちデータの総和をデータの個数で割り算した値を “真ん中” の指標としましょう．図1の上に30標本から計算した平均値（＝11.9）を横線（太実線）で記入すると次の図2が得られます．

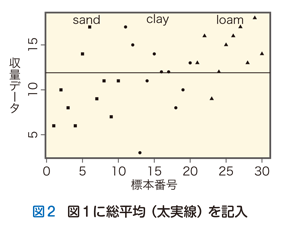
このデータセット全体の位置を示す総平均（grand mean）を“真ん中”を示す基準として，次にそれぞれのデータが総平均から見てどれほど大きな“ばらつき”をもつかが可視化できます．各データと総平均とのこの差を全偏差（total deviation）と定義します．この全偏差は，データが総平均よりも大きければ正の値をもち，逆に平均値を下回れば負の値をもちます．図2に全偏差を書き加えれば次の図3になります．

以上で，データセット全体の挙動を知るために“真ん中”すなわち総平均と“ばらつき”すなわち全偏差という2つの“サーチライト”によって光を当てました．

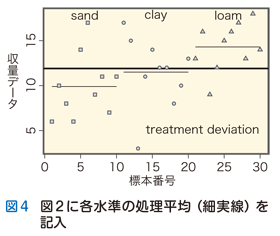
さて，この実験では栽培土壌を三水準で変化させてその効果を調べています．観察された収量データの値がばらつく原因は実験処理水準の結果でしょうか，それとも偶然誤差に起因したのでしょうか．総平均および全偏差という2つの“サーチライト”だけではこの問いに答えることはできません．水準ごとに限定してデータの挙動をより詳細に探査するためには，水準ごとに計算された処理平均（treatment mean：ある水準のデータ総和÷反復数）という“サーチライト”が必要になります．実際に水準ごとに処理平均を計算すると下記のようになります：「sand」＝9.9，「clay」＝11.5，「loam」＝14.3．総平均と処理平均との差は処理偏差（treatment deviation）とよばれます．この処理平均を図2に記入すると図4になります．

太実線で示された総平均がデータセット全体の“真ん中”を示す基準値であるのに対し，細実線で示された処理平均は各水準に限定された“真ん中”を示す基準値といえます．同じ“サーチライト”ではあっても，総平均と処理平均ではその射程の広さに違いがあります．

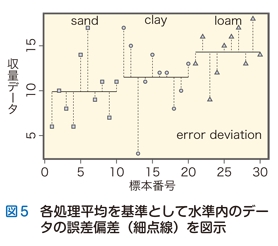
処理平均によって各水準ごとの“真ん中”が確定したならば，各水準内のデータの“ばらつき”を誤差偏差（error deviation：水準内データ−処理平均）として表示できます（図5）．

このように，元のデータセットに対して“真ん中”を示す平均と“ばらつき”示す偏差という2つの“サーチライト”を導入することで，データセットのふるまいに関する「可視化」がきわめて直感的に実現されることが理解できるでしょう．データのもつ“ばらつき”は数値のままでは可視化できません．しかし，上で示したように一つひとつグラフ化することによって，私たちは“ばらつき”のもつ構造を直感的に理解することができるようになります．次回以降に登場することになる水準間の差の検定あるいは分散分析（analysis of variance）という方法の基礎には，データの“ばらつき”こそ情報ソースなのだという信念があるのです．

意外なことに統計学の歴史を振り返ると，データセットの“真ん中”の指標として「平均」を用いるという考え方は17世紀以前にはまったく見当たらないと統計学史家イアン・ハッキングは指摘しています：

平均化という概念自体が新しいものであり，1650年以前には人々は平均をとらなかったので，平均を観察できた人はほとんどなかったのである （文献1，p.155より引用）．

直感的に理解しやすい平均でさえ歴史的に新しい概念であるとしたら，平均を踏まえたデータのばらつきの指標を考えつくのがさらに遅れたとしても不思議ではありません．

指標としての平均と偏差は数値的なデータ解析のスタートラインをも与えます．直感的なデータ解析から定量的な統計分析への移行に複雑難解な数学は必要ありません．私たちに求められているのは，自らの目でしっかりデータを見る姿勢にほかならないのです．

統計的推論はアブダクションである

全数調査のように母集団をすべて調べ尽くす状況では，データセット（＝母集団）は集められた全情報の要約という記述統計としての意味をもちます．一方，母集団からの有限個のサンプル抽出を考える推測統計の場合には，ばらつきのある，すなわち変動のあるデータに基いて，母集団に関する未知パラメーター（真の平均や分散の値）を推論するという状況が生じます．通常のデータ解析は有限個の標本データに基づく推測統計を意味しているので，既知の知見から未知のものを推論するという過程が必ず含まれます．

データ解析の第一段階であるデータの可視化はその後に続く統計的推論の方向づけをするきわめて重要な意義を担っています．実験や観察によって得られたデータはそのまま鵜呑みにはできません．データに含まれているかもしれないさまざまな間違いやノイズ，ばらつきや偏りは，データを蓄積しさえすればいつの間にか真実に到達できるという“バケツ理論”の素朴な実証主義とは相容れません．むしろ，観察されたデータを批判的に吟味することにより，必要に応じて“サーチライト”を照射しながらデータのふるまいを調べるスタンスが必要でしょう．

データ解析を踏まえた統計学的推論「アブダクション（abduction）」という推論形式にしたがっています．推論様式としてのアブダクションは，伝統的な帰納や演繹とは異なり，データを説明するために立てられた仮説の真偽を問いません．同一のデータを説明しようと競合する複数の仮説の間で，データを証拠とする相対的なランキングを与え，それを踏まえてもっともよい仮説を選び出します．

歴史学者カルロ・ギンズブルグはデータがもつ情報的価値について次のように述べました：

資料は実証主義者たちが信じているように開かれた窓でもなければ，懐疑論者たちが主張するような視界をさまたげる壁でもない．いってみれば，それらは歪んだガラスにたとえることができるのだ （文献3，p.48より引用）．

ギンズブルグはデータを鵜呑みにしたり頭から拒否することなく目の前のデータ（資料）を批判的に検討する態度が必要だと強調しました．データが仮説に対してもつ証拠として価値を認めるギンズブルグの結論は統計学の立場からも吟味する価値があります：

ひとは証拠を逆撫でしながら，それをつくりだした者たちの意図にさからって，読むすべを学ばなければならない （文献3，p.46より引用）．

データという “歪んだガラス” を通して見るということは，データと仮説のいずれに対しても 「真偽」 を問うことなく，もっと弱い論理的関係を両者の間に置くことです．それはまた，目の前にある観察データをそれぞれの対立仮説がどれほどうまく説明できるかを数値化し，その善し悪しによってランキングするという意味でもあります．証拠としてのデータが仮説に与える経験的支持は，演繹や帰納が含意する論理的真偽に比べればはるかに弱い関係ですが，それでもなおデータによる仮説の選択力は失われてはいません．われわれは証拠によってより強く支持される仮説を選ぶという基準を置くことができるからです．

データを十分に「逆撫で」したうえで最良の仮説へのアブダクションをすることが統計学の最終目標です．そのためには，何の熟慮もなく単に「計算」するのではなく，前もってデータをよく 「見る」 心構えが私たちには求められています．統計解析に先立つデータ処理の“核心”は「視覚化」にあります．生のデータの挙動がよく“見える”ようなグラフを描くこと，そしていろいろなグラフを併用して視点を変えてデータを“見つめる”ことは，私たちの直感的な“統計センス”と生得的な“認知的能力”のもつ利点を積極的に活用したデータ解析の第一歩となります．

では，データの視覚化に続く次なる一歩とは何か．次回は確率分布とパラメトリック統計学に関する話題に移ることにしましょう．

文献

1. Ian Hacking：The Emegence of Probability: A Philosophical Study of Early Ideas about Probability, Induction and Statistical Inference, Second Edition, 2006
   『確率の出現』（イアン・ハッキング／著　広田すみれ，森元良太／訳），慶應義塾大学出版会，2013
2. Karl R. Popper：Objective Knowledge: An Evolutionary Approach. Clarendon Press, 1972
   『客観的知識：進化論的アプローチ』（カール・R・ポパー／著　森博／訳），木鐸社，1974
3. Carlo Ginzburg：Rapporti di forza: storia, retorica, prova. Giangiacomo Feltrinelli Editore, 2000
   『歴史・レトリック・立証』（カルロ・ギンズブルグ／著　上村忠男／訳），みすず書房，2001