Smart Lab Life

シェア

Tweet

第3回 データのふるまいをモデル化する

統計的モデルをつくるのは人間である

統計的データ解析と聞けば，ふつう，データを統計学的に「説明」することと思われるでしょう．では，ここでいう「説明」とはいかなることなのか．それについてまずはじめに考えてみましょう．観察データを前にした私たちは，データからいったい何が言えるのかについてあれこれ考察を重ねます．

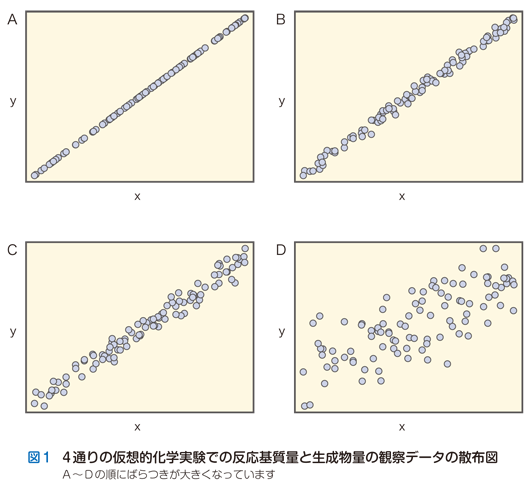
たとえば図1の仮想例を見てください．この図は，仮想的な化学実験での反応基質量と生成物量の観察データの散布図で，それぞれの実験では生成物量の偶然的ばらつきの大きさが異なっています．いずれの仮想実験でも，反応材料である基質量を変化させたときに反応後の生成物量がどのように変化するかを調べるために，各100回の実験をくり返しました．得られた観察データは散布図中の◯で表示されています．

たとえば，生成物量のばらつきがない図1Aの実験結果を見たとき，私たちは直感的に基質量と生成物量との間には“正の比例関係”，すなわち基質量が増えれば生成物量も比例して増えるという直線状の相関性を強くイメージします．生成物量のばらつきがより大きい図1B，Cでも，まちがいなく大半の読者は同様の“正の比例関係”のイメージを抱くでしょう．ばらつきが最大の図1Dになると，ちょっと見ただけではわかりづらくなりますが，それでも“正の比例関係”をイメージすることは困難ではないはずです．

可視化されたデータを説明するために私たちが仮定（イメージ）する変量間の関係性，これがまさしく「モデル」とよばれるものです．得られたデータをどのように説明できれば，すなわちどのようなモデルを想定すれば私たちは納得できるのか．統計学のリクツや数式を持ち出す前に，私たちはデータとの「対話」を通して可能性のある「モデル」を心のなかで造形する必要があります．前回までの記事で私が「生のデータをさまざまなグラフを用いて視覚化するのが先決である」と強調したのは，データとのこの視覚的な対話が統計的データ分析の次の一歩となるモデルの構築を左右するからです．

統計学の立場から図1についてもう少し詳しく見直しましょう．この仮想実験では，基質量と生成物量という2つの変数 〔正確には確率変数（random variable）あるいは変量（variate）とよぶ〕 の間に何らかの「直線的関係」があるというモデルを仮定しても問題ないということです．この直線的な関係性を数式によって表現するならば，基質量（X）と生成物量（Y）に対する，Y＝aX＋b（aとbは定数）という一次関数となります．一次関数によって記述される統計モデルは線形モデル（linear model）とよばれ，統計モデリングのなかではもっともよく用いられるタイプのモデルです．

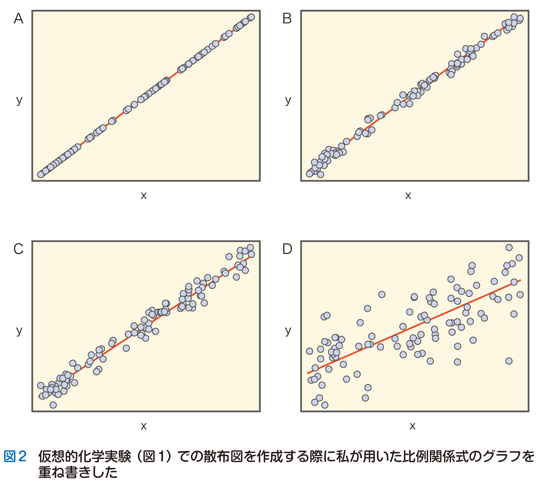
実際に図1を作図したとき，私は 「生成物量＝基質量」 という直線的比例関係の式を与えたうえで，生成物量にランダムなばらつきを付加しました．つまり，私が与えた式は 「生成物量＝基質量＋ばらつき」 となります．図2では，図1の各実験ごとに私が設定した比例関係の式のグラフを重ねました．読者のみなさんはこの式の直線が自分が予想したイメージ（すなわち線形モデル）から大きく外れていないことに安心したのではないでしょうか．

モデルと本質：既知から未知へのアブダクション

しかし，データ解析の現場では変量間の関係を支配する“真”の式はいつまでも未知のまま現象の背後に隠れています．私たちにできることはデータとの視覚的対話を通して，自分が立てたモデルがどれほど説得力のある説明を提示できるのかをアブダクションを通して明らかにすることだけです．

では，観察データに対して想定されたモデルを当てはめることにより，私たちはいったい何を説明しようとするのでしょうか？ 図1の有限個のデータ点に対して直線モデルを当てはめるとき，私たちはある信念を発動しています．それは，観察データの背後には不可視の一般的な関係性・規則性（本質）が潜んでいて，それが現実世界に可視化された結果，すなわち観察データの生起を支配しているという信念です．

図1の例でいえば，基質量と生成物量との間には直線的な比例関係があるという“本質的”な規則性があって，個々の観察データ点はこの本質的関係性から生み出されたという信念を支持しています．もちろん，図2を見ればすぐにわかるように，ある基質量のもとで直線的な比例関係から期待される生成物量と実際に観察された生成物量との間には違いがあります．しかし，その違いは背後に潜む直線的な比例関係が間違っていることを意味するのではなく，現実のデータはランダムなばらつき（誤差）をともなって出現しているからだと解釈されます．「生成物量＝基質量＋ばらつき」という私たちのデータ解釈は，「実現値＝期待値＋誤差」という統計学的思考の根源と深く結びついているのです．

観察データの背後には不可視の本質（essence）があるという信念は心理学的本質主義（psychological essentialism）とよばれています．私たちが想定するモデルは観察データを説明するための「心理的本質」を可視化しているとみなすならば，心理的本質主義の観点から統計学における「説明」の意味がすっきりと理解できます．私たちはもともとばらつきをもったデータ点を一つひとつ別々に理解することはありません．むしろ，データの集まり（データセット）の全体を一挙に説明できる共通要因（心理的本質）を仮定し，その共通要因を通してより単純な説明を試みます．

データ解析における「モデル」はまさにこの要求に応えているといえるでしょう．複雑な現実を単純なモデルによって説明しようとするのは私たちの側の事情であって，現実世界が単純であるからとは決していえません．むしろ，私たちのもつ認知的特性と整合性の良い単純なモデルによる説明を妥当なものとして受け入れていると考えるべきでしょう．

図1のデータを見ただけでは決して図2の“真”に到達することはできません．たとえ自明であるように見えたとしても，私たちが行っていることはあくまでもアブダクションという推論です．図2を見て安心できたとするならば，それは私たちが既知のデータから推論したモデルが，仮想実験を実行したときの“真”の変量間関係と一致したからにほかならないからです．

推測統計学におけるアブダクションは，有限個の観察データという既知の情報に基いて，背後にひかえる未知の母集団に関する推論を行ないます．そのためのツールが，これまで述べてきたモデルです．推測統計学でのモデルは，抽出された標本（サンプル）のふるまいを支配していると仮定される母集団の一般的規則性を明示化したものです．アブダクションという推論を通じて，データのばらつきを確率分布という数式によって記述したり，母集団の未知パラメーターをデータに基づいて推定するパラメトリック統計学の世界に私たちはすでに足を踏み入れているのです．

よりよいモデルとは何か？

既知から未知への跳躍をもくろむアブダクションには「心理的本質主義」の発動が求められます．観察データをじっと見つめる私たちは，既知の情報断片を何とかうまくつなぎあわせて未知の説明原理や法則性を導出しようとします．運よくデータを“きれいに”説明できるモデルが構築できる見込みがあるならば，そのとき私たちは現実世界での観察データを支配する不可視の“本質”をつかむことができたという信念をもつでしょう．この意味で，統計モデルは人間のもつ心理的本質主義を映す鏡であるということができます．

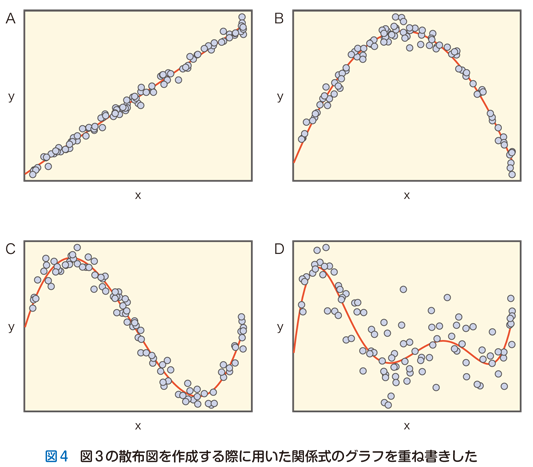
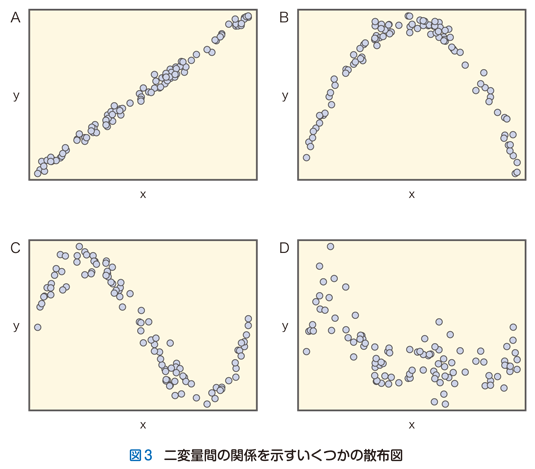
図1と図2では変量間の単純な直線的関係性を例にとって，データとモデルとの関係について説明しました．それよりも複雑な例を図3にあげました．この図3Aは，図1と同じく，変量間の直線的関係性をモデルとして採用するならば容易に説明できるでしょう．しかし，図3Bの場合はそうはいきません．この場合は何らかの曲線的な関係式をモデルとして要求されるでしょう．同様に，図3Cの場合はより複雑な曲線関係をもとに説明しなければならないでしょう．それでも，図3Bならばモデルとして二次関数を当てはめ，図3Cならば三次関数を当てはめる読者がきっと多いのではないでしょうか．しかし，図3Dのケースでは，当てはめるべきモデルに関する読者の意見はわかれるにちがいありません．

単純な図1の状況では表面化しなかった問題点が，ここで浮上してきます．それはある観察データに対してどのようなモデルを当てはめるべきかは先験的には決めることができないという点です．図3の作図をする上で私が用いた“真”の変量間関係を重ね書きすると図4のようになります．図3D以外の3つのケースについてはおそらく大半の読者の予想通りでしょう．しかし，図3Dの関係式をデータから推察することは誰にとっても不可能だったにちがいありません．

アブダクションは可能なモデル群からデータに照らして“ベスト”を選び出すことであると述べました．図3D以外の3つの場合は，現実味のあるモデルは最初から1つしかなかったので，相対的な判定をするまでもありません．しかし，図3Dの場合は当てはまりそうなモデルの選択肢はいくつかあるでしょう．このケースの“真”の変量間関係は五次関数によって支配されています．したがって，ある程度の高い次数をもつ関係式はアブダクションの対象として列挙できるでしょう．

アブダクションは「真実」を言い当てる予言を行なうのではなく，観察データを説明するには選択肢中のどのモデルが「よりよい」かを比較検討する推論作業です．ここでいう「よりよいモデル」とは「より真実に近いモデル」とはかぎりません．むしろ，既知の知見から未知への推論の観点に立って，どのモデルが“ベスト”であるかを考えることが肝要です．例えば，図3Dにおいて，関数の次数を上げてモデルをもっと複雑にすれば，データとの当てはまりももっとよくなるでしょう．しかし，複雑すぎるモデルはデータのちょっとしたノイズや変動に過敏になりすぎるという弊害があります．統計モデルのよしあしの評価基準については，のちの連載で説明するつもりです．

科学哲学者 Elliott Sober は，アブダクションに基づくデータからの推論には最節約原理（the principle of parsimony）が重要であると論じます（文献，Sober 1988）．数ある対立モデルの中から，できるだけ“単純”なモデルを用いてデータを説明するという最節約原理は，哲学の世界では，長らくオッカムの剃刀（Occam’s razor）とよばれてきました．複雑なモデルではなくより単純なモデルをもってデータを説明しようと試みることは，統計学的データ解析にとってきわめて重要な選択基準です．

母集団から抽出されたサンプルのデータに対してアブダクションをどのように進めればいいのか．次回はデータのばらつきの数値化を足がかりにして，パラメトリック統計学の中核となる確率分布について説明することにしましょう．

文献

• 「Reconstructing the Past: Parsimony, Evolution, and Inference」（Elliott Sober），The MIT Press, 1988
• 「過去を復元する：最節約原理，進化論，推論」（エリオット・ソーバー／著　三中信宏／訳），勁草書房，2010