統計の落とし穴と蜘蛛の糸
著/三中信宏
第4回 パラメトリック統計学への登り道① ─ばらつきを数値化する
はじめに
ばらつきのあるデータを前にして私たちがなすべきことは,このデータからどのような結論を導き出すかということです.しかし,データからの合理的推論という作業は,ギリシャのアポロン神殿の神託のような紛れもない「真実」を探し求めることではありません.本連載でくり返し登場する 「アブダクション※」 という推論は,真実を突き止めることをめざしてはいません.アブダクションによって今あるデータのもとで最も妥当な結論を選び出したとしても,さらにデータが蓄積されたならば,その結論は実は間違っていたことが後になってわかるかもしれないからです.むしろ重要なことは,この世のどこかにあるかもしれない真実をむなしく探し続けるのではなく,ある時点で下せる最もリーズナブルな結論を重視しようとする姿勢にあるでしょう.
前回は,データと“対話”するよりどころとして「モデル」という概念を提示しました.統計的データ分析を進めるうえでモデルをどのように設定するかはたいへん重要です.多くの読者は,統計モデルというと,複雑で難解な数式で表現されるものという先入観を抱くでしょう.しかし,前回説明したように,モデルはばらつきやノイズのあるデータを前にした私たちが,どのような規則性やパターンを思い描けばうまい説明ができるかどうかという心理的な要因から,自然と発せられるものです.直感的にうまい説明をするために統計モデルはたいへん役に立ちます.
統計モデルはパラメトリック統計学の中核です.現実世界の現象から得られたデータからいかにして“数理的”に推論を進めるかにパラメトリック統計学は関心を向けてきました.今回は,そのパラメトリック統計学へとつらなる参道を登りはじめます.データのばらつきの数値化を目指して第一歩を踏み出しましょう.
平均値から平方和へ
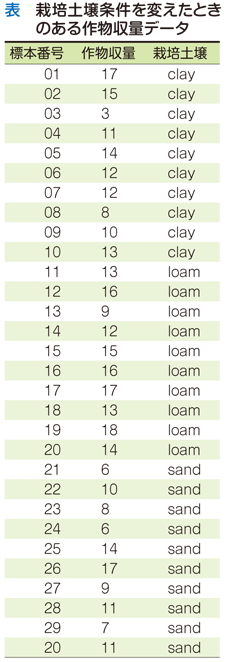
本連載の初回に,統計学者ジョン・テューキーが開発した箱ひげ図について解説しました.データのふるまいを直感的に視覚化する箱ひげ図は今なお広く用いられています.箱ひげ図を作図する基本的な考え方は,データを大小順に並び替えたときの“真ん中”をあらわす中央値(メディアン)を基準として,データのばらつきを「箱」,「ひげ」,および「外れ値」として表示しました.以下では,パラメトリック統計学の観点から,箱ひげ図によって視覚化されたデータのふるまいがどのように数値化されるのかを考えましょう.用いる例は第1回でとりあげた栽培土壌条件を変えたときのある作物収量データです.
この例では,3通りの栽培土壌条件での作物収量を各10標本ずつ測定したデータが得られました(表).計30個のデータから平均値を計算するのはきわめて容易です.この平均値は中央値に代わる数値化された“真ん中”の指標です.第2回では,この平均値から見て各データがどのようにばらつくかに着目してデータセットのふるまいを視覚化しました.
それでは,このばらつきはどのように数値化できるでしょうか?
それは 「データ値-平均値」 によって定義される偏差(deviation)を用いるのが適切です.ここで問題になるのは,各データが平均値から正または負の方向にどれだけずれるかは偏差によって数値化できても,データセットが全体としてどれくらいのばらつきをもつかはそれだけではわからないという点です.
データ点一つひとつのもつ偏差はどのように“集計”すればいいのでしょうか?
単に“集計”するだけであれば,すべての偏差をそのまま足しあわせればいいではないかとつい考えてしまいますが,そのやり方には大きな欠点があります.全データの偏差の総和は「データ値総和-平均値╳データ数」です.ところが,平均値はもともと「データ値総和÷データ数」なので,偏差の単純な総和「データ値総和-平均値×データ数」はゼロになってしまいます.偏差の符号は,データが平均値よりも大きければプラスに,小さければマイナスになります.偏差の総和をとると正負が全体として相殺してゼロになってしまうということです.これではデータ全体のばらつきの“大きさ”を数量的に評価できません.
平方和はばらつきを数値化する
私たちがいま知りたいのは,各データが平均値からどれくらい離れているかの“大きさ”であって,偏差の正負そのものではありません.偏差の符号を取り去る最も簡単な方法はその絶対値を計算することです.それぞれのデータごとに得られる偏差の絶対値の符号は非負ですから,偏差絶対値を総計すれば,確かにデータセットのばらつきをあらわす数値は求まるでしょう.ただし,絶対値を計算するには,偏差の正負によって場合分けをしなければならないのが面倒です.
そこで考案されたのが,偏差の絶対値ではなくその平方値を求めるという方法です.各データごとに計算された偏差を二乗(平方)したうえで,全データにわたってその偏差平方の総和を求めます.二乗した時点で偏差平方は必ず非負の値になり,しかも基準である平均値から離れるほどその値は大きくなります.したがって,この偏差平方和(sum of squares,略して「平方和」と記されます) はデータ全体の平均値からのばらつきを数値化する尺度として適しています.
平方和も視覚化できる
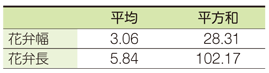
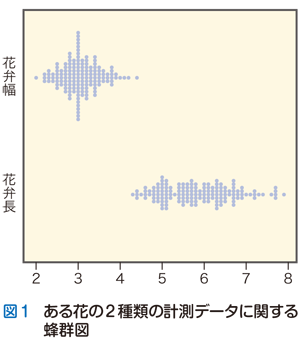
平方和の視覚的イメージをお見せしましょう.ある花の「花弁幅」と「花弁長」を150標本について計測したあるデータセットについて,この2つの計測項目をセンチメートル単位で図示したのが図1です.ここに用いたグラフは
蜂群図を用いると,この2 つの計測データがどのようにばらついているかが一目で視覚化できます.実際に平均と平方和を計算すると次のようになります(単位はセンチメートル).
実測値では平均の位置がそれぞれの蜂群図で異なります.いま,平均がゼロになるようにデータをセンタリング(各データ点からデータセットの平均値を引く)すると,次の図2のようにもっと見やすい図になります.
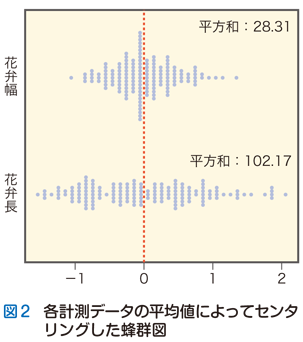
センタリングした結果,それぞれの計測データセットは平均値ゼロ 赤の破線で示す)になります.平方和の値はセンタリングしても変わらないので, 各データセットの平方和がより直感的に理解しやすくなりました.データセットの平方和の大小はデータが平均からどれくらい遠くまでばらつくかの視覚イメージとうまく連動しています.平方和がより小さい花弁幅データセットは,平方和がより大きな花弁長データセットよりも,平均まわりの狭い範囲にばらつきが限られていることがわかります.
このように2 つのデータセットが同数のデータを含んでいるときには,上で説明したように,蜂群図と平方和が直感的にわかりやすい結果になります.ところが,次回で説明するように,データセットによってデータ数が異なる場合には,平方和は必ずしも私たちの直感とは合致しなくなってしまいます.今回はデータセットのばらつきを数値化する方法として平方和を,ばらつきを視覚化する方法として蜂群図をご紹介しました.次回はばらつきの尺度である平方和がデータ数の影響を受けることを解説し,自由度という重要な概念を導入します.
- ※アブダクションとは
- アブダクションという推論様式では提唱された仮説(理論や説明)の「真偽」は問題ではありません.それは得られたデータのもとでどの仮説が 「ベスト」 なのかを客観的に相互比較するということです.伝統的な論理学での推論様式には演繹と帰納の2つがありました.演繹と帰納は対極的に見えますが,仮説の真偽にこだわるという点では違いがありません.一方,アブダクションは,対立する仮説それぞれの真偽ではなくそれらを互いに競り合わせてよりすぐれた仮説に軍配を上げるという点で決定的な違いがあります1).データのもとでの対立仮説間の競争であるアブダクションは,終わりのない推測の連鎖です.なぜなら,新しいデータが次々に登場するとき,以前はベストと判定された仮説が覆される可能性が常にあるからです2).データが更新されるたびに結論が変わりうるアブダクションは統計科学の精神である「既知から未知への推論」を具現しています.
文献
- 1)「系統樹思考の世界:すべてはツリーとともに」(三中信宏/ 著),講談社,2006
- 2)「進化思考の世界:ヒトは森羅万象をどう体系化するか」(三中信宏/ 著),NHK 出版,2010