統計の落とし穴と蜘蛛の糸
著/三中信宏
第5回 パラメトリック統計学への登り道② ―自由度とは何か
はじめに
データのもつ“ばらつき”の情報をいかに利用するかは統計的データ解析の根幹です.前回はこの“ばらつき”をいかに数値化するかを解説しました.今回はその続きで,データセットの“ばらつき”を視覚化する平方和についてさらに説明を続けます.個々のデータの「偏差」を集計して「平方和」を計算すれば,データセット全体の“ばらつき”が一つの数値で表されます.しかし,平方和はデータセットの大きさ(サイズ)をまったく考慮しません.その欠点を解決するために,「自由度」という新しい概念が必要になります.データを集計するだけの記述統計学とは違って,データが取られた元の集団(母集団)に関する推定をする推測統計学にとって,データからの推定が真の値にどれほど近いかは重要な問題です.自由度を用いることで,私たちははじめて“ばらつき”の尺度である推測統計学的に妥当な「分散」の概念に到達できます.データセットのふるまいを表す「平均」と「分散」が数値化されることにより,パラメトリック統計学の参道の終点が見えてきます.
平方和はデータ数に影響される
前回,それぞれのデータの偏差平方を集計した平方和という数値尺度を使えば,どんなデータセットであっても,ばらつきの程度を数値化することができるということを紹介しました.ここで問題になるのは,異なるデータセットの間でばらつきの程度を比べるにはどうすればいいのかという点です.確かに,それぞれのデータセットについては平方和の値さえあれば十分でしょう.しかし,2つのデータセットのばらつきの大きさを比較しようとするとき,単に平方和の大きさを比べるだけでは十分とはいえません.偏差平方の総和である平方和という統計量はデータ数という重要な要因を全く考慮していないからです.
データセットの「データ数」の違いをどのように補正して,より “公平” なばらつきの比較をすればいいのでしょうか.
まずはじめに,そもそもデータ数が平方和の大きさにどれほどの影響を与えるかを実際にお見せします.図1Aの2つのデータセット(前回も使用した,ある花の「花弁幅」と「花弁長」のデータセット)はともに150個という同数のデータを含んでいます.ここで,花弁長データ計150個から無作為に30個のデータ点を抽出するという操作をします.花弁長データを元の5分の1のサイズに減らすということです.実際にこの操作をした結果を図1Bに示します.
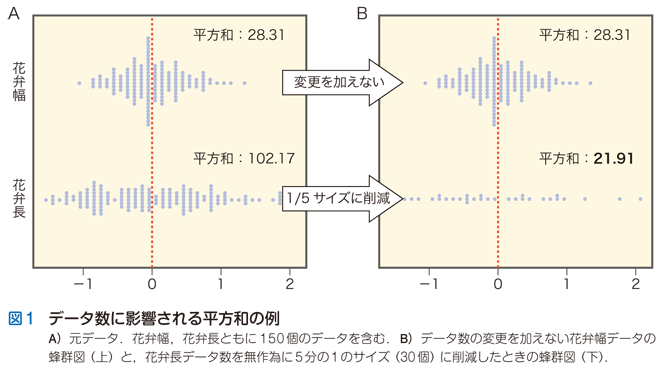
データ数が150個のままの花弁幅データと5分の1のサイズに削減した花弁長データの蜂群図を平均値でセンタリングしてこのように並置すると,データのばらつきに関していえば,範囲がより狭い花弁幅データよりも,横に広がる花弁長データの方が “直感的” にはより大きいことがすぐにわかります.ところが,実際に平方和を計算すると,5分の1に削減された花弁長データは「21.91」となります.削減されない花弁幅データは「28.31」でしたから,見かけのばらつきと平方和の値とは逆の結果を示します.
このような “逆転” が生じる原因は平方和のもつ基本性質にあります.平方和は個々のデータがもつ偏差平方をデータセット全体にわたって足し合わせて求めます.平均値まわりのごく狭い範囲にデータの分布が集中しているとき,一つひとつの偏差平方は小さな値であったとしても,データ数が十分に大きければ総和としての平方和の値はより大きくなるでしょう.一方,平均から遠くにまで散らばっているデータセットの場合,確かに個々の偏差平方は大きな値を取るでしょうが,データ数が小さいならば,集計した平方和としてはデータ数が大きいデータセットにはかなわないかもしれません.データ数の違いを考慮しないという点で,平方和はデータの “ばらつき” の数値尺度として大きな欠陥をもっているということです.
では,複数のデータセットの “ばらつき” を互いに比較するとき,データ数の違いをどのように補正すれば,より “公平” な比較が可能になるのでしょうか.
データセット間で比較できるばらつきの指標へ
高校数学「確率・統計」の検定教科書1)に書かれているやり方は,平方和をデータ数で割り算するという方法です.例えば,2つのデータセットのサイズがそれぞれ10と100であったとき,各データセットから計算された平方和を対応するデータ数で割り算することで “補正” するわけです.この方法は直感的にとてもわかりやすいという利点があります.平均を計算するときに,データの総和をデータ数で割り算するのと全く同じやり方で,偏差の平方和をデータ数で割り算すればいいからです.ところが話はそう簡単ではないのです.データ数で割り算すると不適切な結果をもたらす簡単な数値例をお見せしましょう.
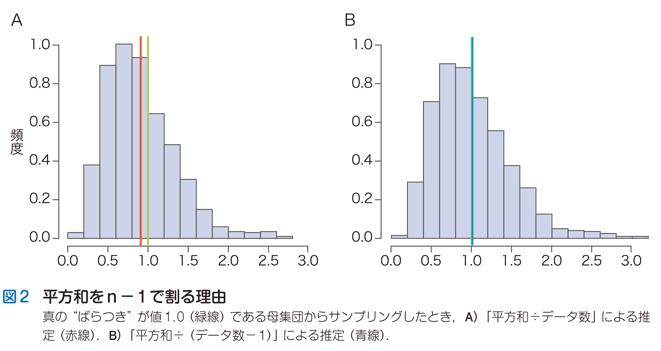
この図2Aは, “ばらつき” の値が正確に「1.0」(緑線)であることがわかっている無限個のデータ集団から,無作為に10個のデータを抽出するというシミュレーションを1,000回くり返して得た結果です.縦軸は頻度(density)を表しています.シミュレーションによって得られた1,000個の平方和をデータ数10で割り算した値のヒストグラムとその平均を赤線で示しました.すぐわかるように,平方和をデータ数10で割った値は真の値1.0よりも小さくなり,過小推定しています.「平方和÷データ数」という “補正法” では,この実験で最初に与えた “ばらつき” の真値を正しく導くことはできないようです.
次の図2Bは,図2Aと全く同じシミュレーションに対して,平方和を「データ数-1」で割った値のヒストグラムとなります.その平均は青線で示しました.平方和を「データ数-1」で割ると,“ばらつき” の真値にきわめて近い値が得られることがわかります.このシミュレーションを何回くり返しても,真の緑線により近いのは青線であり,赤線は常に過小推定してしまうという傾向にかわりはありません.
「データ数-1」は自由度(degree of freedom)とよばれます.統計学を学ぶうえで,この「自由度」という概念は難物であるようで,私は過去にくり返し次のような質問を受けた経験があります:
次の節ではこの疑問への回答をしましょう.
自由度はパラメトリック統計学に通ず
私たちはそもそも何のために平均や平方和を計算するのでしょうか.それは統計学の根幹にかかわる問題です.例えば,目の前に10個の数字(データ)があるとき,そのデータの特徴を集約する目的で平均を計算したり,平方和を求めることができます.これは 記述統計学(descriptive statistics)的な統計計算の考え方です.記述統計学がめざすところは,データの特性や挙動を数値的に描き出すことです.そして,記述統計学の世界にとどまるかぎり,データセットの “ばらつき” をそのデータ数によって補正することには何も問題はありません.
ところが,前述の数値シミュレーションは,記述統計学ではなく,推測統計学(inferential statistics)という別の目的をもった統計学に属しています.推測統計学とは観察者の目の前にあるデータの背後に広がる母集団(population)に関する推測を行うための方法論を指しています.前述のシミュレーションをもう一度見ると,記述統計学と推測統計学との違いがはっきりします.ここで想定している「母集団」とは “ばらつき” の値が1.0であることがわかっている無限個のデータの集まりです.そこから無作為に10個のサンプルを抽出するという操作をしています.有限個のサンプルから母集団の “ばらつき” に関する推定をするのがここでの推測統計学のゴールになります.一方,記述統計学は目の前の10個の数値データの集約をするだけで,背後の母集団に関する推論は眼中にありません.たとえば全国民の年齢や性別などを調べる国勢調査は,典型的な全数調査なので,記述統計学が扱うべき対象となります.一方,生物学や医学での研究の多くは,有限回の実験結果に基いて一般的な結論を推測あるいは予測するので,推測統計学が使われる機会がほとんどでしょう.
平方和をデータ数で割るという計算は,たとえ記述統計学的には妥当であったとしても,推測統計学的には母集団の “ばらつき” に関する正しい推定値を導きません.それでは,推測統計学の観点からみて平方和の妥当な “補正法” とは何かが次の問題になります.
妥当な補正法としての不偏分散
母集団から無作為に抽出された標本(データ数をnとしましょう)は互いに無関係(統計学では互いに独立とよびます)なので,平均を計算する際にデータの総和をデータ数nで割り算して “真ん中” を決めるのは全く問題ありません.
しかし,平方和の場合はそうはいきません.前回説明したように,無作為抽出された標本から計算された偏差の総和はゼロになってしまいます.したがって,n個のデータから計算されたn個の偏差のうち,いずれか1つは他のn-1個の偏差によって決定されてしまいます.見かけはn個の偏差がありますが,実際に “自由” に値がとれる偏差はn-1個しかありません.この「n-1」という値こそが,平方和のもつ自由度というわけです.要するに,平方和をデータ数nで割るのは “割り過ぎ” ということです.図2Aが示すように,「平方和÷データ数(n)」が真の値に対して常に「過小推定」の傾向がある原因はここにあります.
「平方和÷自由度(n-1)」で定義される値を不偏分散(unbiased variance)とよびます.図2Bからわかるように,私たちは,母集団から抽出されたサンプルに基いてこの不偏分散を計算することにより,母集団の真のばらつきを偏りなく推定することができます.パラメトリック統計学の理論によると,妥当な平方和の “補正法” は「平方和÷自由度(n-1)」であることが数学的に証明されているのですが,今回は数値シミュレーションを使ってその結果をみなさんに示しました.
母集団から無作為抽出されたサンプルは推測統計学の情報源です.パラメトリック統計学はサンプルから得られる情報を活用すべく,さまざまな理論とツールを開発してきました.2回にわたってデータのもつ平均と分散という2つの尺度を通じて,パラメトリック統計学が構築される足場を築きました.平均と分散という基本的な尺度はデータの数理モデル化(確率分布)にとって重要な役割を果たします.次回はいよいよ確率分布が織りなすパラメトリック統計学の世界に話を進めることにしましょう.
文献
- 1)「高等学校の確率・統計」(黒田孝郎,森 毅,小島 順,野崎昭弘/著),筑摩書房,2011