3 エネルギーと運動量

- 物理学における仕事を理解する.
- 力学的エネルギーを理解する.
- 力学的エネルギー保存則を理解する.
- 運動量保存則を理解する.
仕事
 てこを使うと重いものを小さな力で動かせてよいというが,逆に大きくなるものはないか?
てこを使うと重いものを小さな力で動かせてよいというが,逆に大きくなるものはないか?
 てこを使うと重いものを小さな力で動かせてよいというが,逆に大きくなるものはないか?
てこを使うと重いものを小さな力で動かせてよいというが,逆に大きくなるものはないか?日常生活では,やらなければならないことや職業などで「仕事」という言葉を使う.物理学でも「仕事」という言葉を使うが,その場合の「仕事」とはどういうものか見ていこう.
3.1.1仕事
❶仕事とは
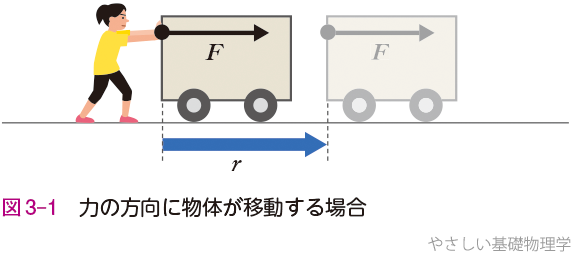
物理学では力が物体を動かしたとき,「力が仕事をした」という.例えば,図3-1のように一定の大きさの力\(F\)で物体を押して力の方向に距離\(r\)動かしたとすると,力\(F\)が物体にした仕事\(W\)は
\(W=Fr\)……(3.1)
で定義される.力を加えても,物体が動かなければ仕事をしたことにならない.単位は[N・m] = [J](ジュール)※1 である.すなわち,\(F\)=1 N,\(r\)=1 mとすると,\(W\)=1 N・1 m=1 Jとなる.
※119世紀に熱やエネルギーの研究で活躍したイギリス人物理学者James Prescott Joule(1818-1889)にちなむ.詳しくは4章参照.
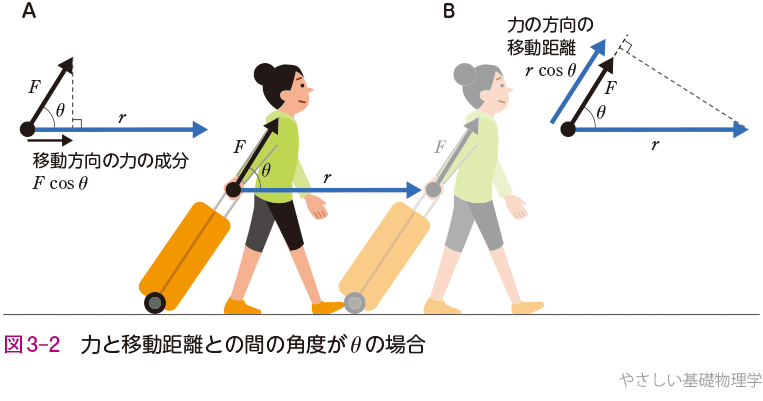
❷力の方向と物体の移動方向が斜めになる場合の仕事
図3-2のようにキャリーバッグを引いて歩くとき,腕が引く力とキャリーバッグの移動方向は同じではない.その間の角度を\(θ\)とすると,力\(F\)が移動する物体にした仕事\(W\)は,図3-2Aに示すようにキャリーバッグが移動した方向の力の成分\(F\) cos\(θ\)に移動距離\(r\)をかけたものとなる.すなわち,
\(W=F\) cos\(θ×r\)……(3.2a)
となる.あるいは,図3-2Bに示すように,力の大きさ\(F\)と力の方向に沿った移動距離\(r\) cos\(θ\)を用いて,
\(W=F×r\) cos\(θ\)……(3.2b)
となる.このように2通りの見方ができるが,結局,仕事\(W\)は同じ式で表される.
\(W=Fr\) cos\(θ\)……(3.2)※2
(3.2)式は仕事を求めるうえで,力の方向と移動方向が任意の場合の一般式である.
※2力や移動距離(変位の大きさ)をベクトル量として考えると,仕事は正確には力ベクトルと変位ベクトルとの内積で定義される.すなわち,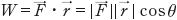 (ただし,\(θ\)は
(ただし,\(θ\)は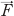 と
と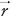 とのなす角)である.この定義式から(3.2a)式,(3.2b)式のいずれも定義どおりであることがわかる.
とのなす角)である.この定義式から(3.2a)式,(3.2b)式のいずれも定義どおりであることがわかる.
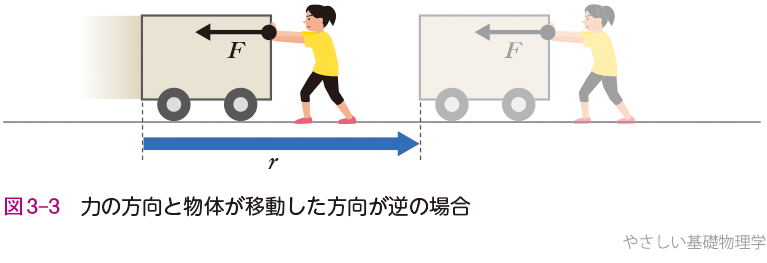
❸力の方向と物体が移動した方向が逆の場合の仕事
図3-3のように,動いている荷車に対して逆向きで一定の大きさの力\(F\)で押し続けたところ荷車は静止,あるいは減速した.力を加え続けた距離を\(r\)とすると,力\(F\)のした仕事は荷車の移動方向とは逆,すなわち,(3.2)式において\(θ\)=180°の場合となるので,
\(W=Fr\) cos\(180°=\)-\(Fr\)……(3.3)
となる.このように,物体の移動方向と逆向きの力を加えて,物体が静止したり減速したりした場合,力がする仕事は負となる.
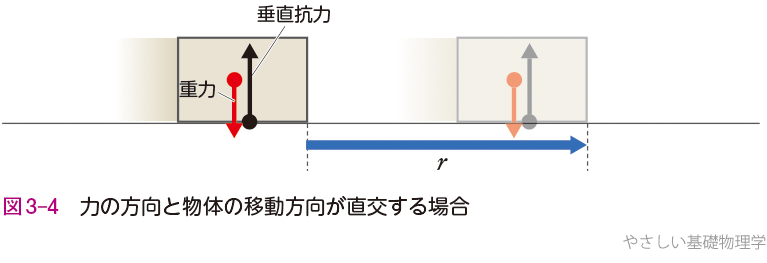
❹力の方向と物体の移動方向が直交する場合の仕事
図3-4のように水平な床面を移動する物体にかかる重力や垂直抗力は仕事をしない.なぜなら,(3.2)式において\(θ\)=90°の場合に相当するためである.
\(W=Fr\) cos\(90°=0\)……(3.4)
このように,力の方向と移動方向が直交する場合の仕事は0になる.
3.1.2仕事の原理
てこを使うと重いものを小さな力で動かせてよいというが,逆に大きくなるものはないか.ここで,図3-5のようなてこを考えよう.質量\(m\)の物体を高さ\(h\)だけ持ち上げる.支点Oと作用点Aの間の距離を\(a\),支点Oと力点Bの間の距離をその2倍の2\(a\)とする.
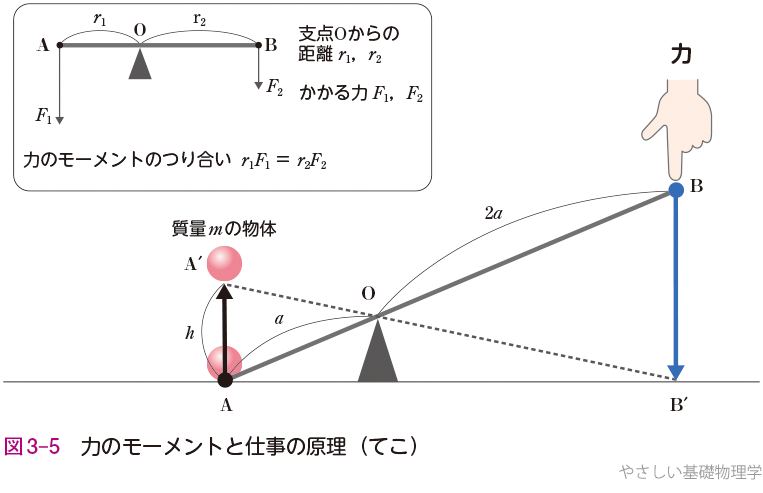
次に1章の “力のモーメントのつり合い” を思い出そう.重力加速度を\(g\)とすると,A点にかかる力のモーメント\(r_{1}F_{1}=amg\)である.一方,力点Bにかける力の大きさを\(F\)とすると,A点とつり合うB点の力のモーメントは,\(r_{2}F_{2}=2aF\)であるから
\(r_{1}F_{1}=r_{2}F_{2}\)
\(amg=2aF\)
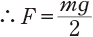
よって,B点での力の大きさはA点の物体にかかる重力の半分でよい.
では,物体にかかる重力の半分よりわずかに力を大きくして,物体を動かそう.ただし,図3-5の△AOA′と△BOB′は相似なので,BB′=\(2h\)となり,物体を距離\(h\)持ち上げるためには力を2倍の距離加え続けなければならない.このように,てこを使えば力は小さくてよいが,その代わり動かす距離は大きくなる.このときの仕事を\(W\)てことすると
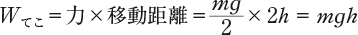
である.一方,てこなどの道具を使わずに\(h\)だけ持ち上げる場合は,同様に物体にかかる重力よりわずかに大きな力を加える必要があるが,力を加え続ける距離は\(h\)である.このときの仕事を\(W\)とすると
\(W=\)力×移動距離\(=mg×h=mgh\)
となる.このように道具を使っても使わなくても仕事が変わらないことを仕事の原理という.
3.1.3仕事率
同じ仕事でも短時間で済む場合と長時間かかる場合がある.仕事率は単位時間あたりの仕事として定義される.すなわち,仕事率\(P\)は,仕事を\(W\),かかった時間を\(t\)とすると,
 ……(3.5)
……(3.5)
で表すことができる.単位は[J/s]=[W](ワット)※3 である.すなわち,\(W\)=1 J,\(t\)=1 sとすると,\(W\)=1 J/1 s=1 J/s=1 Wとなる※4 .
※3蒸気機関の発展に貢献したイギリス人発明家James Watt(1736-1819)にちなむ.
※4電子レンジなどの電気製品でよく[W](ワット)という単位を見かける.これは消費電力の単位であり,電力も仕事率として定義されている.詳しくは8.3.2参照.

・仕事\(W\)[J] \(W=Fr\) cos\(θ\)
(\(F\)[N]:力の大きさ,\(r\)[m]:移動距離,\(θ\):力の方向と移動方向のなす角度)
・仕事の原理:てこなどの道具を使っても仕事は変わらない.
・仕事率\(P\)[W] \(P=W/t\)
(\(W\)[J]:仕事,\(t\)[s]:仕事をするのにかかった時間)
 図3-2のようにキャリーバッグを運ぶとき,
図3-2のようにキャリーバッグを運ぶとき,
①腕と水平な床との間の角度を60°とすると,10 Nの力で120 m移動した場合の仕事を求めよ.
②①の仕事をするのに1分かかったとする.そのときの仕事率を求めよ.
 ①600 J ②10 W
①600 J ②10 W
ご覧ください

