専門家同士なら「ほら，あれ」「ああ，あれな」ですむ．そばで聞いていた専門外の人は「あれってなに？」ってなる．そうならないように深層学習へ進む前に超基本用語を整理したい．本章の見出しをみて「自分はあれで大丈夫」という勇者は，次章に進んでいただいて結構である．そうでない方は，ここはひとつ我慢をして読んでいただきたい．

　人工知能と機械学習と深層学習

人工知能（artificial intelligence，AI）と機械学習（machine learning）と深層学習（deep learning）という3つの用語は本書で頻出する（図1）．

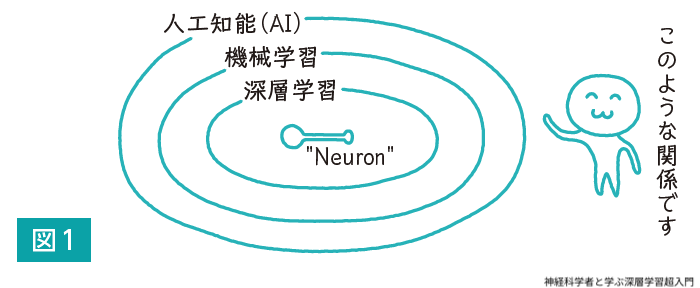
人工知能は最も広い意味合いをもつ．人間の知能をコンピュータで模倣していれば，どんなものでも人工知能とよぶ．特に最近は日常でもよく使われるようになったが，かなり曖昧な用語である．初期の人工知能にはエキスパートシステム（expert system）がある．これは専門家の知識をもとにして「if-then」形式でルールを明示的にして構築していく．「ここに果物があります」「色は？」「黄色」「形は？」「三日月」「じゃあ，バナナですね」という具合である．病気や法律の自動判断など，基本的に人間の知識をベースにして発展してきた．

機械学習は人工知能の一分野であるが，データからパターンをコンピュータで学習し，獲得したパターンからルールを生成して予測や決定を行う．ルールを人間が設定しないでコンピュータに任せるので「機械」学習である．多量のデータからルールを生成することで人工知能の性能を大幅に向上させることができる．機械学習でパターンをコンピュータで学習する際には，人間が設定した関数が駆使されることになるが，その関数に後述する「人工ニューロン（artificial neurons）」を利用すれば深層学習とよばれる．つまり機械学習は人工知能の一分野であり，深層学習は機械学習の一分野である．深層学習では人工ニューロンを多数組み合わせた構造であるニューラルネットワークによって高レベルの特徴抽出や学習を行う．

　モデル

「モデル（model）」という用語についても整理しておきたい．というのは，人工知能にしても機械学習にしても深層学習にしても，その根底にある概念はモデルだからである．モデルという概念がうまく頭に入っていないと，どうしても小手先の理解になる．少し我慢をして読んでいただきたい．

モデルの定義は「現実世界の複雑な事象や系を単純化あるいは抽象化して表現したもの」である．プラモデルを例にするとわかりやすい．プラモデルは，飛行機やアニメの巨大ロボットなどの造形物の外観だけを単純化してプラスチックで表現した玩具である．あくまでも外観だけであるが，巨大なものでも微小サイズのものでも手に取れるサイズに形状を抽出することで，非現実的で複雑なものを自分たちの生活している世界に引き込むことができる．

適用される分野は幅広い．機械の動作であったり，経済理論であったり，自然の法則においても，モデルは活用される．自然科学の世界では，物理学のニュートンの運動方程式やボーアの原子モデル，生物学のDNA二重らせんや進化モデル，天文学の宇宙膨張モデルなどである．3つの基本法則からなるニュートンの運動方程式は数式で書くことができるシンプルな数理モデルであるが，モデルは数式では書けない複雑な対象でも威力を発揮する．例えば，心理現象は非常に複雑であり，モデル研究に大きく依存している．フロイトの心的構造論も，ラッセルの提案した感情円環構造も心理モデルである．心理モデルで現象の理解が進むと同時に，対案を生む土壌もできる．異なるモデル同士を戦わせることで現象の理解がさらに進む．また最近巷でよく使われるビジネスモデルという用語は，企業の利益を生み出すしくみを説明する．ビジネスをモデルとして記述することで汎用性が生じると同時に，企業戦略を簡潔に表現しているので投資家への説明も容易になる．このようにモデルは現象を理解し，予測し，説明するための強力なツールである．

そしてモデルは人工知能の中心的な概念である．旧来の人工知能は，人間の知識をモデル化してきた．機械学習や深層学習は，良いモデルを自動的に生み出すための方法論である．それらは学習可能なパラメータをもち，複雑なパターンを表現し，画像や言語など現実世界の現象をモデル化する．その詳細は後述するとして，まずはモデルという概念を頭に残しておきたい．

最後にモデルによく似た「関数（function）」という用語を追記しておく．関数は入力を受けとり，一定のルールや操作に従って出力を生成する数式，あるいはプログラムのことであり，数式やコードで明確に定義された入出力関係を表現している．この関数を拡張したのがモデルであると考えればよい．念を押すが，モデルは必ずしも関数で書かれている必要はない．込み入ったビジネスのしくみを数式やコードで書くことはできないので，ビジネス関数ではなくビジネスモデルである．その点，深層学習は特異な立場にある．深層学習の根幹にある人工ニューロンやニューラルネットワークは，いずれも数式やプログラムコードで表現することができる．しかしニューラルネットワークが対象としている現実世界はきわめて複雑であり，従来は関数での表現は不可能とされていた領域である．にもかかわらずニューラルネットワークは，その不可能を可能にしつつある魔法の関数なのである．そしてニューラルネットワークは関数であるがゆえに，コンピュータで計算できる．

　線形と非線形

「用語はもういいから，そろそろ人工ニューロンへ進みましょうよ」という声が聞こえてきたような気もするが，もう一息である．図で押し切るので読みやすいと思う．図2左のグラフを見ていただきたい．

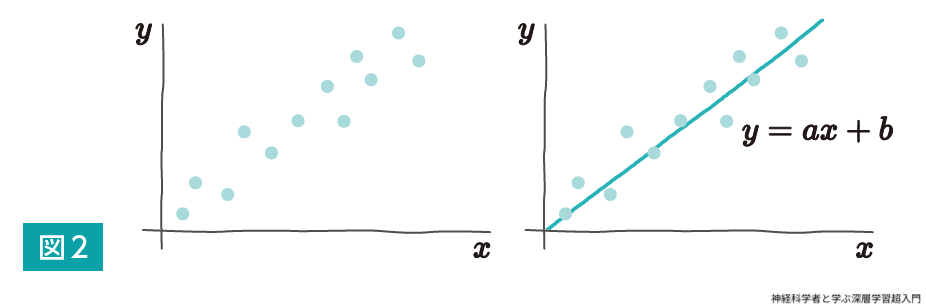
xを体重，yを身長と読み替えていただいてもいい．あるデータをプロットしてみた．生命科学ではよく見る類のグラフである．このグラフをみるとムズムズする．そう，一本の線を引きたくなる（図2右）．これで落ち着いた．このデータは一本の線で「モデル化」できるのである．線の正式な引き方はここでは議論しないが，直線の関数であるy＝ax＋bをコンピュータで自動計算すれば，立派な機械学習である．yとxは比例の関係にあり，これを線形モデルとよぶ．線形モデルは人間にとって最もありがたいモデルで，両者の関係を直感的に理解できる．線形モデルにすることで，未知のxに対してyの値を推定することができる．ここで，y＝ax＋bのyはモデルによる推定値であるということに注意してほしい．真の値は実際の計測データのyである．本書では，真の値yと区別するために推定値は$\hat{y}$と表記する．つまりy＝ax＋bの正式な式は$\hat{y}=ax+b$となる．

さて図2の例はシンプルな線形モデルで表現できたが， 図3のグラフはどうだろうか．

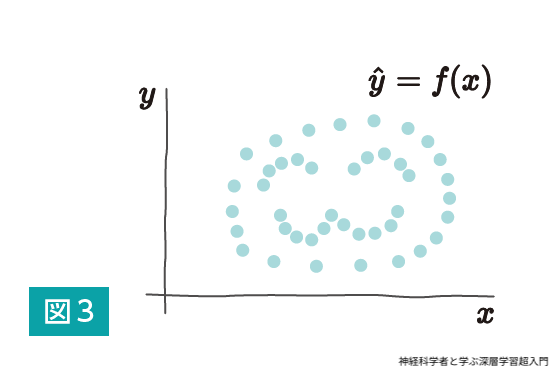
もはや線形モデルで表現できないのは明白である．非線形モデルの出番である．非線形モデルは入力と出力の関係が曲線や複雑なパターンで表現されるモデルの総称である．見たところxとyの関係は，決してランダムというわけではない．何か「ルール」がありそうだ．しかし，$\hat{y}=f\left(x\right)$はどんな関数なんだろう？ 二次関数でも三次関数でもなさそうだ．いよいよ人工ニューロンの出番である．